一、方差、标准差、均方误差(MSE)、均方根误差(RMSE)区别总结
方差(样本方差)是各个样本数据和平均数之差的 平方和 的平均数。
标准差(Standard Deviation),又称均方差,是方差的平方根。
均方误差是各数据偏离真实值差值的平方和的平均数,也就是误差平方和的平均数。均方误差的开方叫均方根误差
那么问题来了,既然有了方差来描述变量与均值的偏离程度,那又搞出来个标准差干什么呢?
原因是方差与我们要处理的数据的量纲是不一致的,虽然能很好的描述数据与均值的偏离程度,但是处理结果是不符合我们的直观思维的。
再举个例子:一个班级里有60个学生,平均成绩是70分,标准差是9,方差是81,假设成绩服从正态分布,那么我们通过方差不能直观的确定班级学生与均值到底偏离了多少分,通过标准差我们就很直观的得到学生成绩分布在[61,79]范围的概率为68%,即约等于下图中的34.2%*2。
(自己的例子:3个人,160,165,170,方差为:(5*5+5*5+0)/3=50/3=16,标准差为:4.0
总结
从上面定义我们可以得到以下几点:
1、均方差就是标准差,标准差就是均方差
2、方差 是各数据偏离平均值 差值的平方和 的平均数
3、均方误差(MSE)是各数据偏离真实值 差值的平方和 的平均数。
4、方差是平均值,均方误差是真实值。
总的来说,方差是数据序列与均值的关系,而均方误差是数据序列与真实值之间的关系,所以我们只需注意区分 真实值和均值 之间的关系就行了。
二、MSE、RMSE、MAE、R-Squared四个指标
回归算法同分类算法不同,回归算法主要用来预测,而分类算法的目的是为了分类,所以两种算法的评判标准当然也不一样。
本文就是从MSE、RMSE、MAE、R-Squared四个指标来谈一谈如何衡量回归算法的好坏。
均方误差 MSE(Mean Squared Error)
均方误差是误差的平方的期望值,而误差是指估计值和被估计值的差。公式如下:


将误差平方
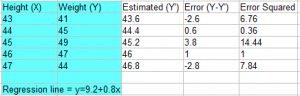
计算期望
将所有平方差加起来除以数量:(6.76 + 0.36 + 14.44 + 1 + 7.84)/ 5 =6.08
代码:
y_predict=reg.predict(x_test) # reg是预测模型 mse=np.sum((y_predict-y_test)**2)/len(y_test)
均方根误差(RMSE)

平均绝对误差 (MAE)


代码实现
r_squared=1-(np.sum((y_predict-y_test)**2)/np.var(y_test))
通过scikit-learn来计算metrics
from sklearn.metrics import mean_squared_error #均方误差 from sklearn.metrics import mean_absolute_error #平方绝对误差 from sklearn.metrics import r2_score#R square #调用 mean_squared_error(y_test,y_predict) mean_absolute_error(y_test,y_predict) r2_score(y_test,y_predict)
Notice
以上三个Metrics不能单独令出一个来衡量模型,因为当一个metric看着很漂亮的时候很容易显示过拟合的状态,那么哪个更好呢?没有觉对的答案。
MAE vs RMSE
RMSE很容易受到极端值的影响,如下个例子:
假设你想了解量女朋友在准时方面的特点,你统计了近两个月女朋友约会的迟到时间(即是实际到达时间和约定时间的差距,或误差,单位可以是分钟,时间有夸大,我们只想你更好理解概念),如下:
第一个月迟到时间1 = ([5, 10, 5, 10, 5, 10, 5, 10, 5, 10, 5, 10, 5, 10, 5, 10, 5, 1000])
第二个月迟到时间2= ([5, 10, 5, 10, 5, 10, 5, 10, 5, 10, 5, 10, 5, 10, 5, 10, 5, 10])
我们计算得出:
对于第一个月:平均绝对误差MAE2=62.5分钟,均方根误差RMSE2:235.82分钟
对于第二个月:平均绝对误差MAE1=7.5分钟,均方根误差RMSE1=7.91分钟
第一个月的平均绝对误差MAE(62.5)与均方根误差RMSE(235.82)之比接近1:4,第二个月迟到时间的平均绝对误差MAE(7.5)与均方根误差RMSE(7.91)之比约为1:1。我们应该用哪个量衡量女朋友守时呢?我们看到均方根误差RMSE受异常值的影响更大。如果我们去评判女朋友守时方面的进步,用RMSE标准,我们更可以看到她的进步之大,也许更要奖励她一顿饕餮盛宴。
一般来说,我们应该期望MAE值比RMSE值小得多。因为对于均方根误差RMSE,每个误差都是平方的。这意味着单个误差呈二次增长,并且对最终RMSE值有不同的影响。
这两组误差序列之间的惟一区别是序列1中的极值是1000,而不是10。因此,我们看到较大的异常值对均方根误差RMSE的影响更大。
原文链接:
https://blog.csdn.net/itslifeng/article/details/108096358
https://zhuanlan.zhihu.com/p/83410946

