一、策略说明:
这是一个小小的Demo。最好在jupyter notebook下面执行,不然图形无法显示。
在cmd执行时如果提示“ No module named 'statsmodels'”,则直接使用“pip install statsmodels ”安装即可。
二、测试结果:
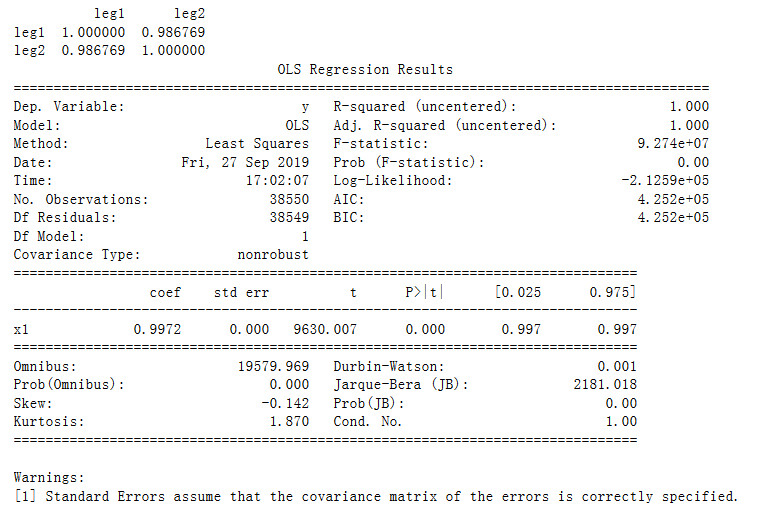
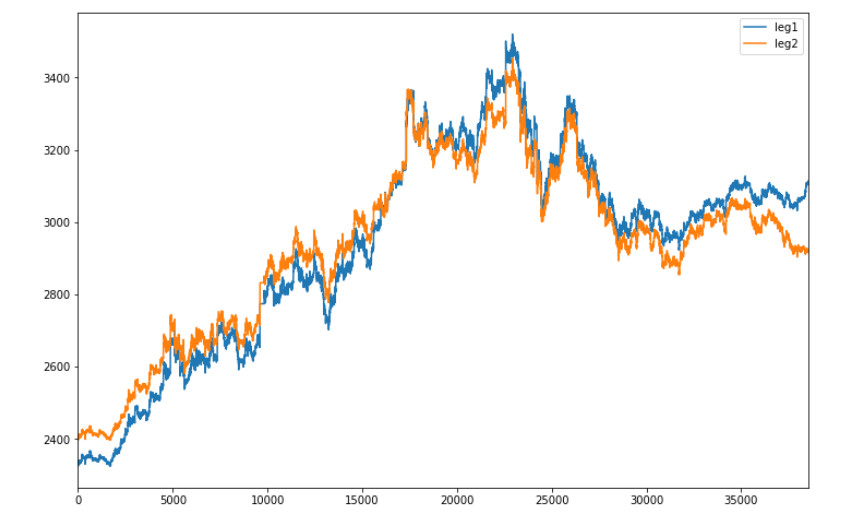
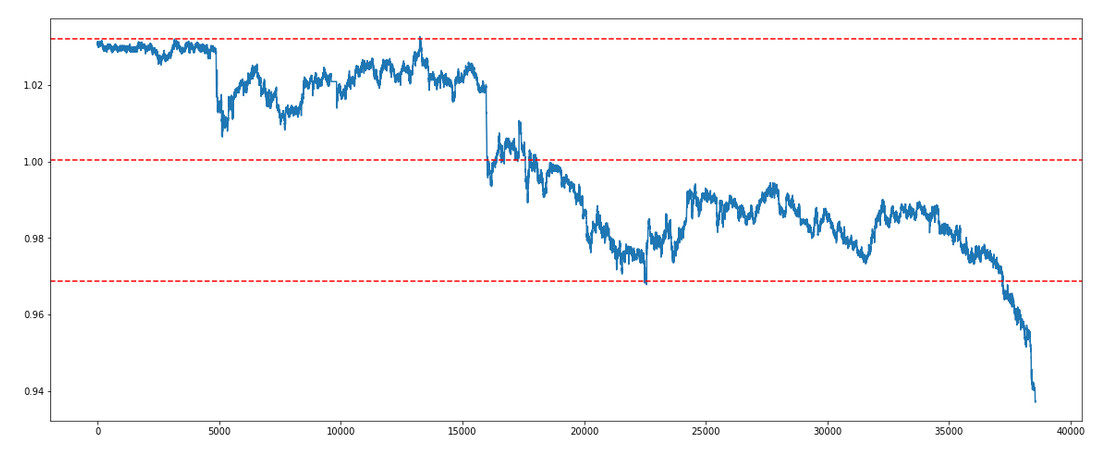
三、代码
import numpy as np
import pandas as pd
import talib as ta
import matplotlib.pyplot as plt
import rqdatac as rq
rq.init()
leg1_symbol = 'M1609' # Leg1
leg2_symbol = 'M1701' # Leg2
start_date = '20160401'
end_date = '20160830'
# 显示走势图,传入df以及要显示的columns,传入格式为['leg1','leg2'],相当于执行df2=df2[['leg1','leg2']]
def display(df,columns):
df2=df.copy()
df2=df2[columns]
df2.index = list(range(len(df))) #生成数字列表作为df2的索引。
df2.plot(figsize=[12,8]) #figsize控制图表的大小,因为df2有leg1,leg2,所以生成的图表上有两条线。
plt.legend() #作用就是给图加上图例
# 显示两个合约的相关度
def display_coor(df,columns):
df2 = df.copy()
df2 = df2[columns]
corr=df2.corr()
print(corr)
# 显示两个合约的协整值,合约配比
def display_ols(df,leg1,leg2):
import statsmodels.api as sm # 最小二乘
columns = []
columns.append(leg1)
columns.append(leg2)
df2 = df.copy()
df2 = df2[columns]
X=df2[leg1].values #取出leg1这一列的值,返回的是numpy.ndarray
y=df2[leg2].values
model = sm.OLS(y, X) # 普通最小二乘模型,ordinary least square model
results = model.fit() #获取拟合结果
print(results.summary())
# 查看两个合约的配比
plt.figure(figsize=[20,8])
plt.plot(y/X) # 利用 leg2/leg1的价格比率,画出线图。 y/X是numpy.ndarray
plt.axhline(np.mean(y/X), color="red", linestyle="--") #axhline绘制平行于x轴的水平参考线
plt.axhline(np.mean(y/X)+np.std(y/X)*1.5, color="red", linestyle="--")
plt.axhline(np.mean(y/X)-np.std(y/X)*1.5, color="red", linestyle="--")
# 读取2个合约的3四个月内的分钟数据,取到的是pandas.core.series.Series
leg1=rq.get_price(leg1_symbol,start_date=start_date,end_date=end_date,fields='close',frequency='1m') # leg1
leg2=rq.get_price(leg2_symbol,start_date=start_date,end_date=end_date,fields='close',frequency='1m') # leg2
leg1.head()
leg2.tail()
df = leg1.to_frame(name='leg1') #执行后df的类型变成了pandas.core.frame.DataFrame
df['leg2']=leg2 #df添中了一列leg2
display(df,['leg1','leg2'])
display_coor(df,['leg1','leg2'])
display_ols(df,'leg1','leg2')
# filename = u'{0}_{1}_{2}_{3}.csv'.format(leg1_symbol,leg2_symbol,start_date,end_date)
# df.to_csv(filename)
四、小知识
1. plt.legend()
plt.legend()函数主要的作用就是给图加上图例,plt.legend([x,y,z])里面的参数使用的是list的的形式将图表的的名称喂给这和函数。
比如,设定["red","Blue"]就会在图表的右上解显示red,blue。
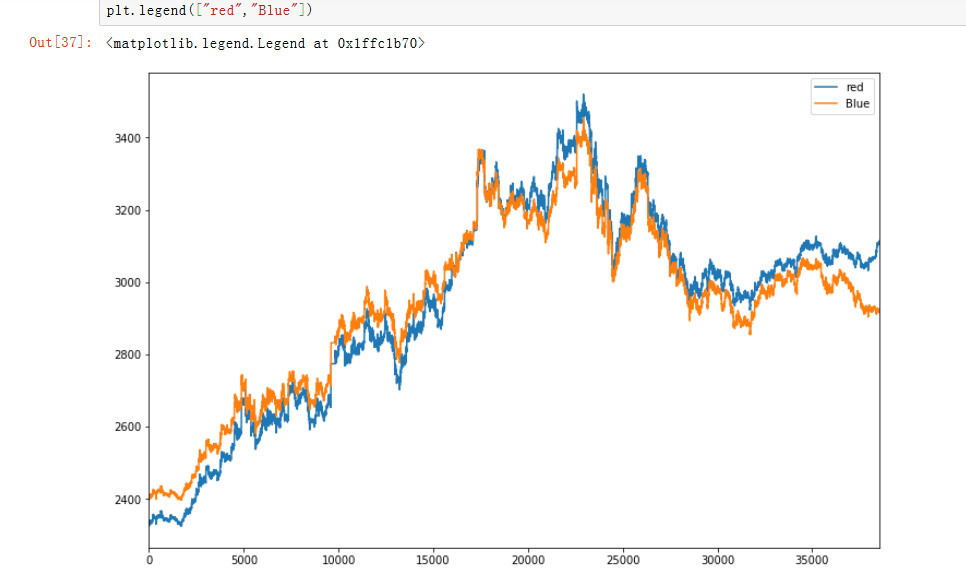
2.corr()
用来刻画二维随机变量两个分量间相互关联程度。
3.Statsmodels
Statsmodels 是 Python 中一个强大的统计分析包,包含了回归分析、时间序列分析、假设检
验等等的功能。Statsmodels 在计量的简便性上是远远不及 Stata 等软件的,但它的优点在于可以与 Python 的其他的任务(如 NumPy、Pandas)有效结合,提高工作效率。
它最常用的就是 OLS(ordinary least square)功能。
4.线性回归
线性回归也被称为最小二乘法回归(Linear Regression, also called Ordinary Least-Squares (OLS) Regression)。它的数学模型是这样的:y = a+ b* x+e
其中,a 被称为常数项或截距;b 被称为模型的回归系数或斜率;e 为误差项。a 和 b 是模型的参数。
当然,模型的参数只能从样本数据中估计出来:y'= a' + b'* x
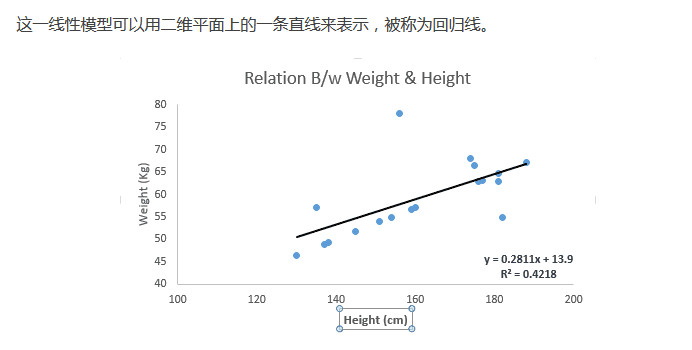
我们的目标是选择合适的参数,让这一线性模型最好地拟合观测值。拟合程度越高,模型越好。
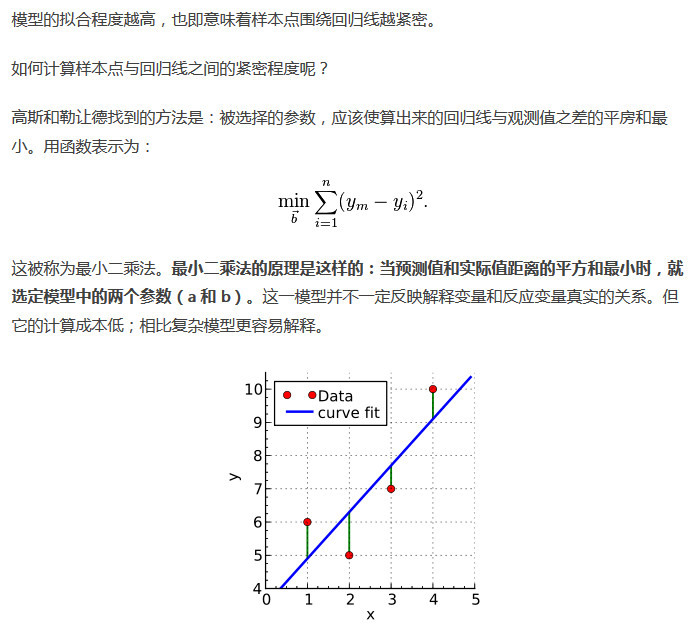
那么,接下来的问题就是,我们如何判断拟合的质量呢?
代码:
import numpy as np import matplotlib.pyplot as plt import statsmodels.api as sm nsample = 100 x = np.linspace(0, 10, nsample) #用于产生x1,x2之间的N点行矢量,相邻数据跨度相同。 X = sm.add_constant(x) #将截距列添加到现有矩阵,在 array 上加入一列常项1 beta = np.array([1, 10]) #系数 e = np.random.normal(size=nsample) #所谓标准正态分布 y = np.dot(X, beta) + e #观察值y np.dot:向量点积 model = sm.OLS(y,X) #最小二乘法 results = model.fit() #拟合数据 print(results.params) print(results.summary())
运行结果
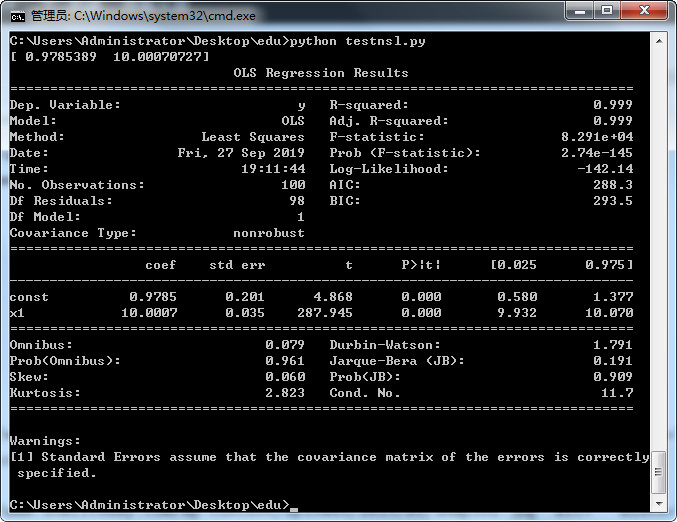
可参考:
https://www.jianshu.com/p/e45558ccf533
https://xueqiu.com/8287840120/75542824

